A Beginner-Friendly Exploration of SVM, VC Dimension, Hyperplanes, Support Vectors, Soft Margins, Kernel Trick, and Multiclass Classification.

The Support Vector Machine (SVM) is a versatile algorithm used for both regression and classification tasks. It’s particularly useful when dealing with numerical random variables. In this post, our focus will be on explaining how SVM works for classification problems. The goal here is to make the explanation as accessible as possible, avoiding excessive use of mathematical proofs and theorems that might seem intimidating. I want to introduce SVM in a surface-level manner so that you can grasp the logic behind it. This way, you’ll be prepared to delve deeper into the subject with a solid understanding of the algorithm’s purpose, or even have a basic comprehension that allows you to apply it quickly.

Vapnik-Chervonenkis (VC) Dimension:

The Vapnik-Chervonenkis (VC) dimension is a measure that assesses the capacity of a set of functions to be learned by a statistical binary classification algorithm. In simpler terms, the VC dimension of a set of functions is the maximum number of points that can be divided in different ways by those functions. This measure was proposed by Vapnik and Chervonenkis in 1971, and it’s extremely useful for understanding the flexibility of a set of functions in the classification task.

Example: The VC dimension of a set of linear functions for classifying 2 groups in a plane is equal to 3.

If we had to perform a binary classification with 4 points, it wouldn’t be possible to find a linear function that separates all possible combinations.

Hyperplane:

A hyperplane is a (k-1)-dimensional plane in a k-dimensional space. For example, in a two-dimensional space, a hyperplane is a line, while in a three-dimensional space, it is a plane.

Connecting with the previous topic, the VC dimension of a hyperplane in a K-dimensional space is equal to K+1. There are multiple possible hyperplanes for classifying the data:

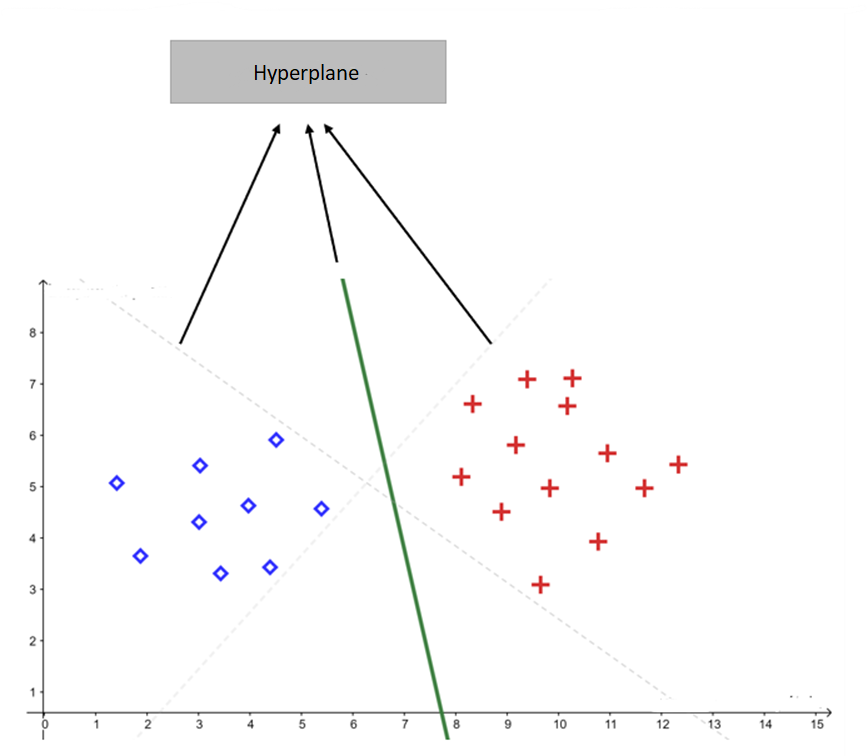
But SVM aims to find the hyperplane with the largest margin of separation between the two classes.

Support Vectors:

Support vectors, also known as critical points, are the data points that assist in determining the margin of the linear classifier. They play a crucial role in identifying the optimal hyperplane.

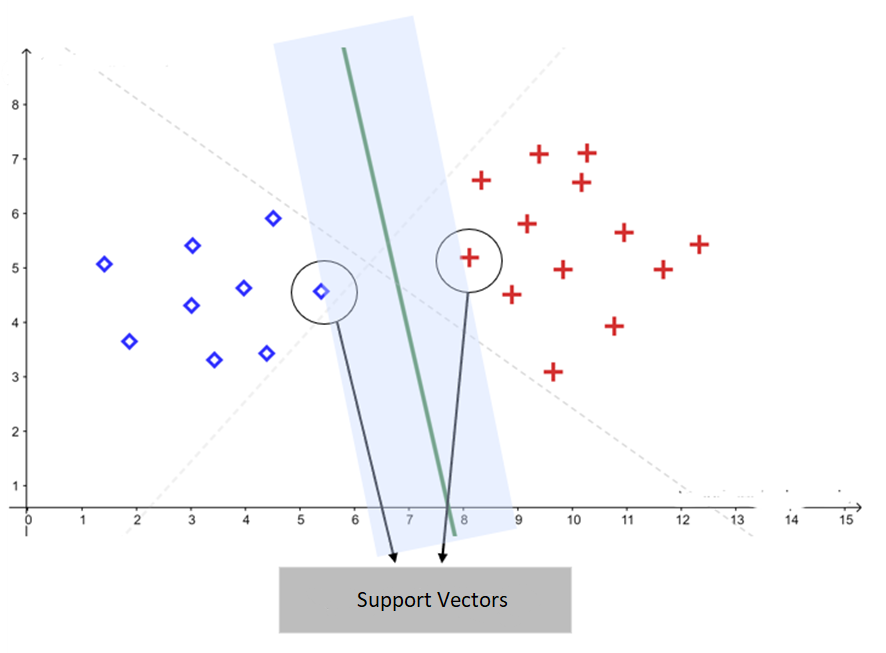
Soft Margins:

To avoid overfitting, it is possible to adopt soft margins, allowing some data points to fall within the separation margin. This flexibilizes the classification and makes the model more robust.

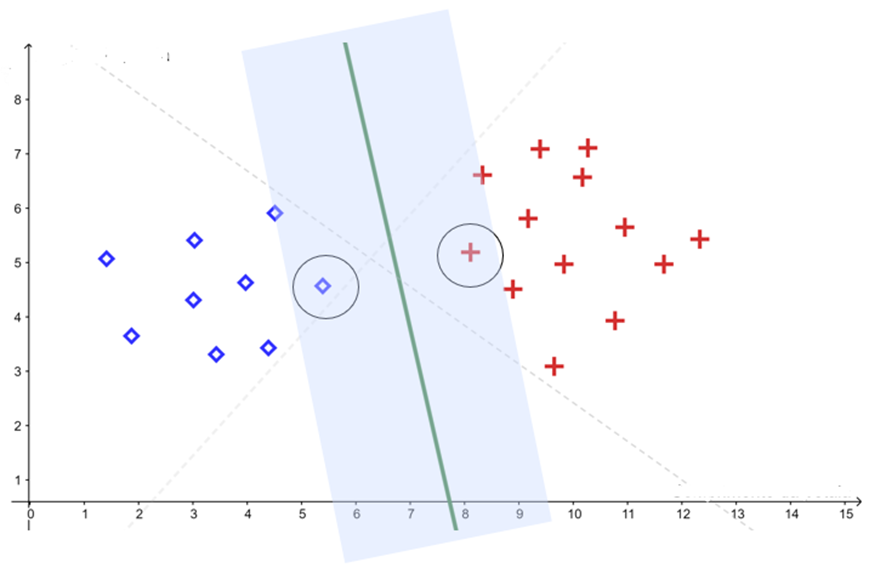
What if the data were distributed differently?

Nonlinear Data and the Cover’s Theorem:

Cover’s Theorem tells us that nonlinear datasets in high-dimensional spaces are more likely to be linearly separable compared to lower-dimensional spaces, as long as the space is not excessively crowded.

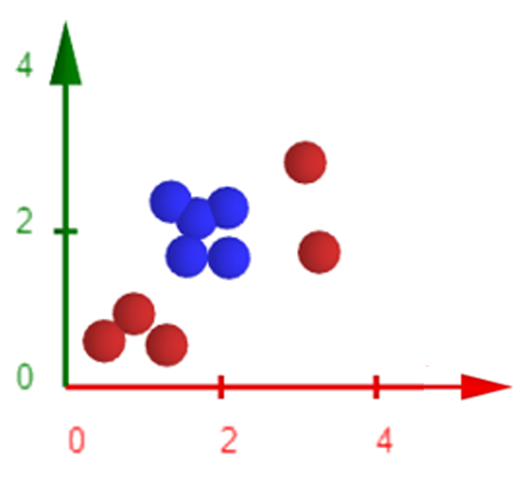
Based on that, we can apply a transformation to the data, such as the function , to map them into a higher-dimensional feature space. This makes it feasible to apply linear SVM in this new feature space.

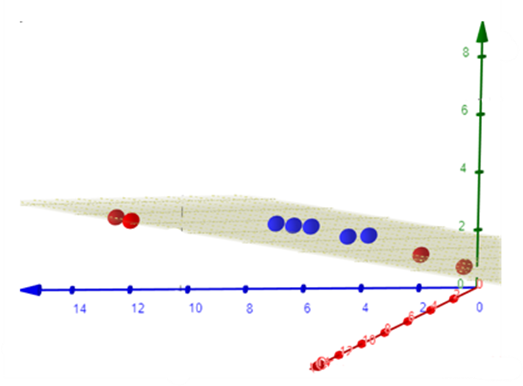
However, it is important to note that computing the mapping function for the feature space can be computationally expensive due to the high dimensionality.

Kernel Trick:

The kernel trick is a technique that allows us to avoid the explicit mapping of data to the high-dimensional feature space. According to the Mercer’s Theorem, the kernel function takes input space points and computes their inner product in the feature space, as long as the kernel is defined as a positive-definite matrix with eigenvalues greater than zero. Illustrating this, we have the kernel that defines the mapping ϕ to a higher-dimensional space. Consider the polynomial kernel function with γ=1, c=0, and d=2. With these parameters, it is known as the quadratic kernel.

The mapping of points to a higher-dimensional space is given by the function:

There are various types of kernel functions, such as polynomial, radial, and hyperbolic tangent. These functions define the mapping to a higher-dimensional space.

Polynomial

Radial

Hyperbolic tangent

But what if we had more than 2 classes to classify?

Multiclass SVM Classification:

SVM is originally designed for binary classification. However, there are methods that allow for the classification of more than two classes.

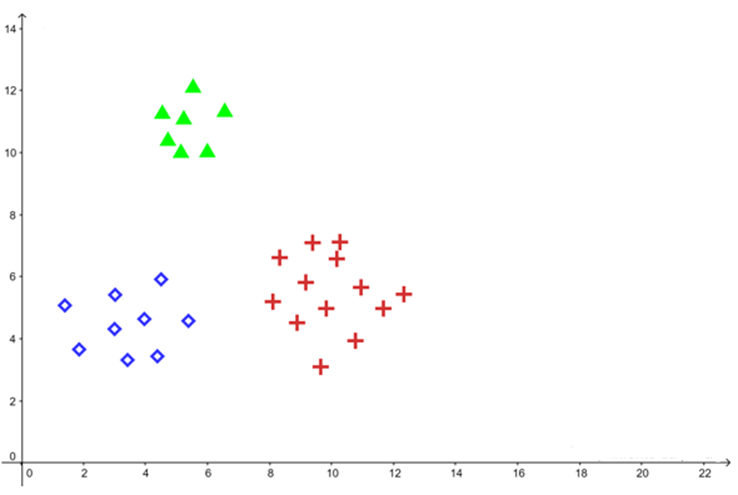
Some of the main methods are:

One-vs-All (One-vs-Rest):

Divides the data into two groups, where one group consists of a specific class and the other group contains all the remaining classes. This is repeated for each class.

One-vs-One:

Calculates the classification between one class and another class. This is repeated for all possible pairs of classes.

Directed Acyclic Graph SVM (DAG-SVM):

It is a generalization of the decision tree, where the tree grows by excluding classes, using binary classification.

In this post, we have explored the workings of the Support Vector Machine (SVM) algorithm for classification problems in an accessible and straightforward manner. I hope you have gained a solid understanding of the logic behind this powerful algorithm and are ready to dive deeper or even apply it to your own tasks.

I would love to hear from you! Please leave your comments below and share your questions, experiences, or any additional insights related to the topic of this post. I’m here to help and would love to start a meaningful conversation with my readers. Your participation is valuable and contributes to the enrichment of our community.

If you have any questions or need further clarification, please don’t hesitate to reach out to me. I am committed to providing support and guidance to all my readers.

I hope this post has been helpful and informative. Thank you for following along!

References:

• Shalev-Shwartz, Shai, and Shai Ben-David. Understanding Machine Learning: From Theory to Algorithms. Cambridge University Press, 2014. [link]

• Faceli, Katti. Inteligência artificial: uma abordagem de aprendizado de máquina. Grupo Gen - LTC, 2011.

• Cover, Thomas M. “Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition.” IEEE Transactions on Electronic Computers, vol. EC-14, no. 3, June 1965, pp. 326–34. DOI.org (Crossref), https://doi.org/10.1109/PGEC.1965.264137. [link]

• Chih-Wei Hsu and Chih-Jen Lin. “A Comparison of Methods for Multiclass Support Vector Machines.” IEEE Transactions on Neural Networks, vol. 13, no. 2, Mar. 2002, pp. 415–25. DOI.org (Crossref), https://doi.org/10.1109/72.991427.

• Platt, John and Cristianini, Nello and Shawe-Taylor, John. “Large Margin DAGs for Multiclass Classification”. Advances in Neural Information Processing Systems, MIT Press, vol.12, 1999. [link]

• V.N. Vapnik and A.Ya. Chervonenkis. Theory of Pattern Recognition. Nauka, Moscow, 1974. (in Russian); German translation: Theorie der Zeichenerkennung, Akademie Verlag, Berlin, 1979.