Uma exploração inicial das SVM, Dimensão VC, Hiperplanos, Vetores de Suporte, Margens Flexíveis, Truque do Kernel e Classificação Multiclasse.

A máquina de vetores de suporte, em inglês Support Vector Machine (SVM), é um algoritmo versátil usado tanto para regressão quanto para classificação. Ele é especialmente útil quando lidamos com variáveis aleatórias numéricas. Neste post, vamos nos concentrar em explicar como o SVM funciona para problemas de classificação.

O objetivo aqui é tornar a explicação o mais acessível possível, evitando o uso excessivo de demonstrações matemáticas e teoremas que possam parecer assustadores. Quero apresentar o SVM de forma superficial para que você possa entender a lógica por trás dele. Assim, você estará preparado para se aprofundar no assunto, já com uma base sólida sobre o propósito do algoritmo, ou mesmo para uma compreensão básica que permita aplicá-lo rapidamente.

Dimensão Vapnik-Chervonenkis (VC):

A dimensão Vapnik-Chervonenkis (VC) é uma medida que avalia a capacidade de um conjunto de funções serem aprendidas por um algoritmo de classificação binária estatística. Em termos mais simples, a dimensão VC de um conjunto de funções é o número máximo de pontos que podem ser divididos de formas diferentes por essas funções. Essa medida foi proposta por Vapnik e Chervonenkis em 1971, e é extremamente útil para compreender a flexibilidade de um conjunto de funções na tarefa de classificação.

Exemplo: Dimensão VC de um conjunto de funções lineares para classificação de 2 grupos em um plano, é igual a 3.

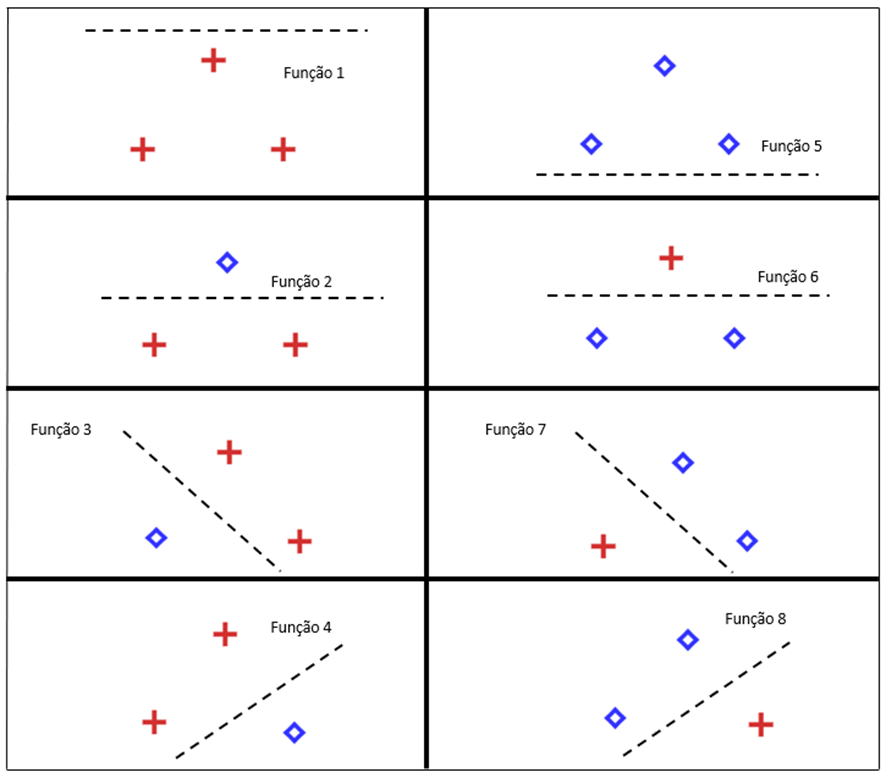
Se tivéssemos que realizar uma classificação binária com 4 pontos, não seria possível encontrar uma função linear para todas as combinações possíveis.

Hiperplano:

Um hiperplano é um plano de dimensão k-1 em um espaço de dimensão k. Por exemplo, em um espaço bidimensional, um hiperplano é uma reta, enquanto em um espaço tridimensional, é um plano.

Conectando com o tópico anterior, a dimensão VC de um hiperplano em uma dimensão K é igual a K+1. Existem vários hiperplanos possíveis para classificar os dados:

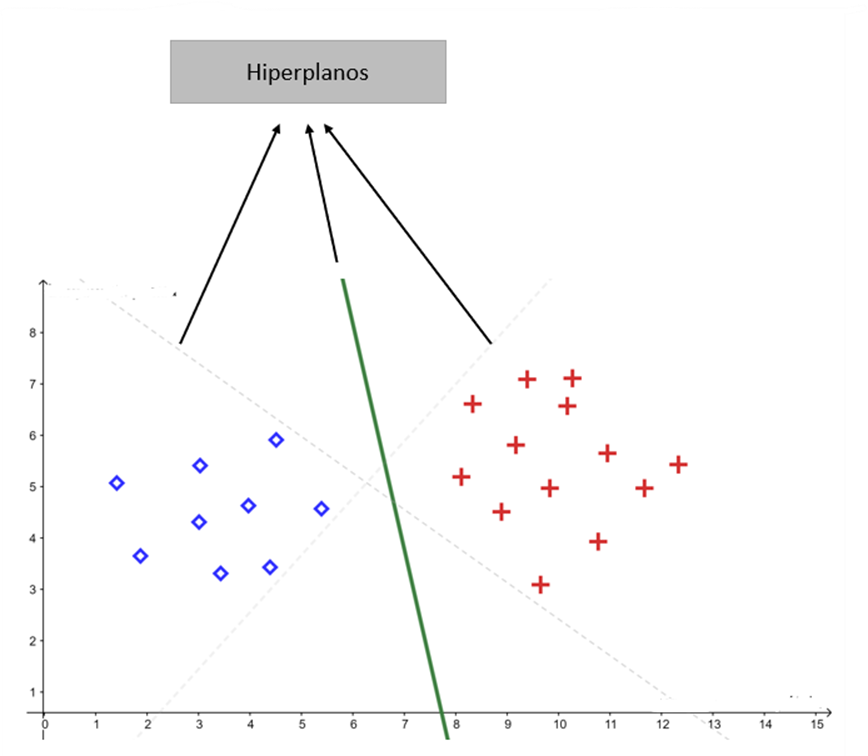
Mas o SVM visa encontrar o hiperplano que possui a maior margem de separação entre as duas classes:

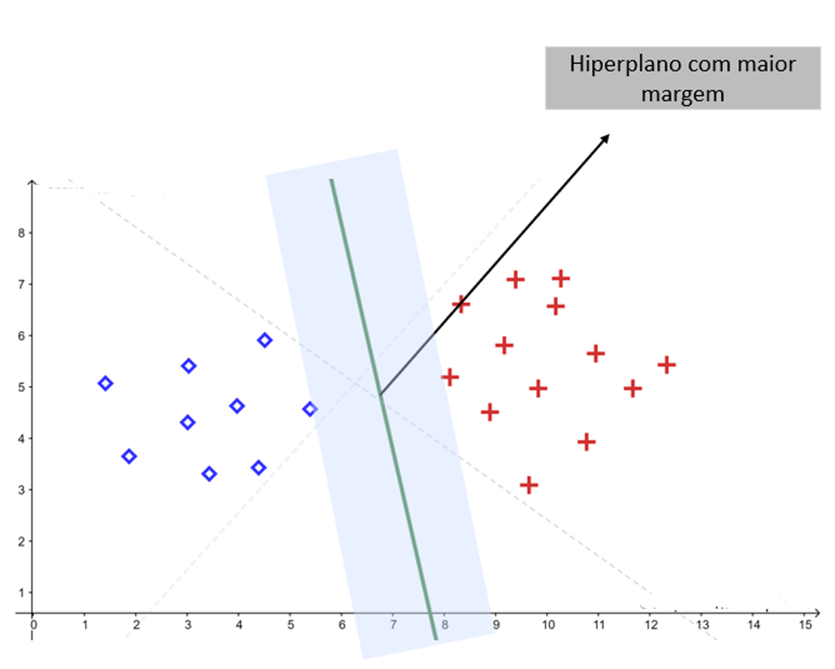
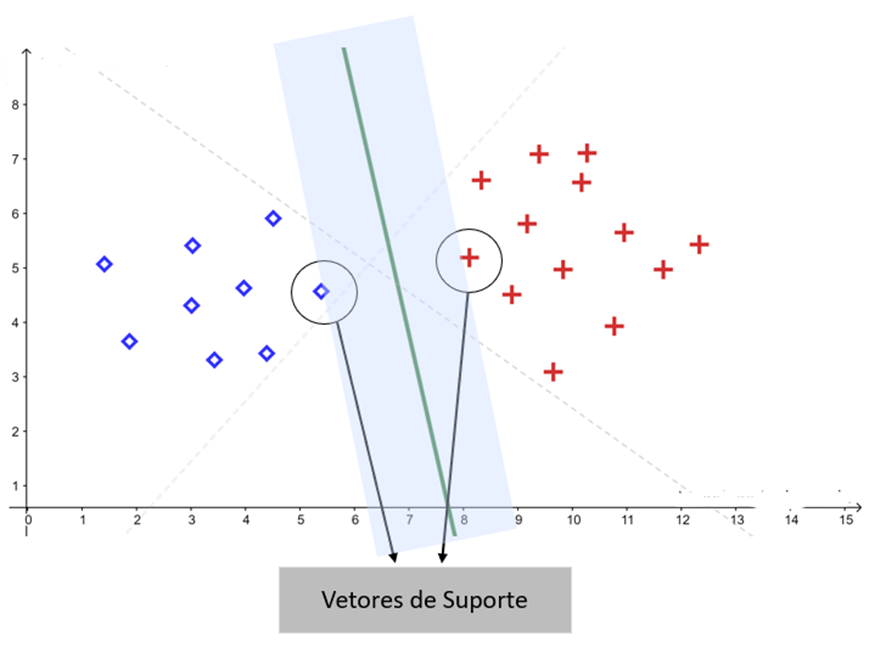
Vetores de suporte:

Os vetores de suporte, também conhecidos como pontos críticos, são os pontos de dados que auxiliam na determinação da margem do classificador linear. Eles são fundamentais para a identificação do hiperplano ideal.

Margens suaves:

Para evitar o sobreajuste, é possível adotar margens suaves, permitindo que alguns pontos de dados fiquem dentro da margem de separação. Isso flexibiliza a classificação e torna o modelo mais robusto.

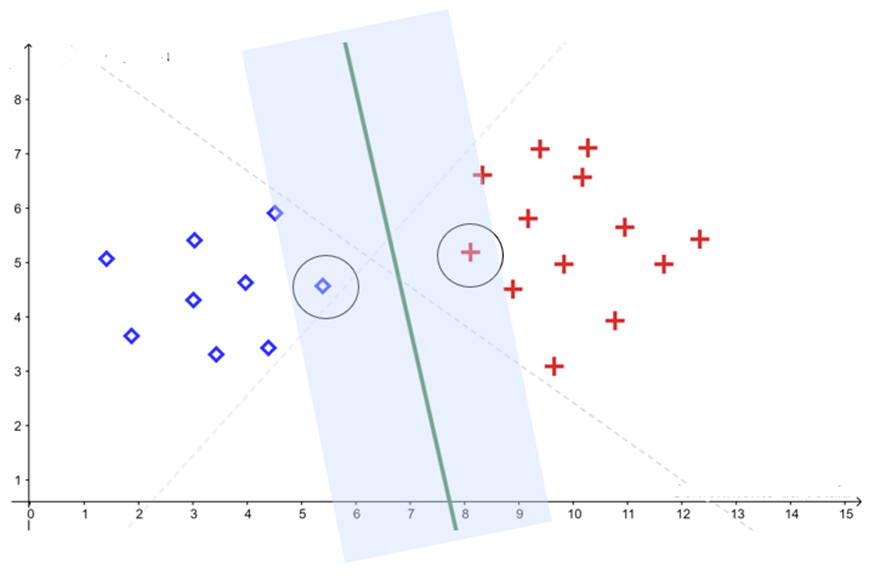
E se os dados fossem distribuídos de outra forma?

Dados não lineares e o Teorema de Cover:

O Teorema de Cover nos diz que conjuntos de dados não lineares em espaços de alta dimensão são mais propensos a serem linearmente separáveis em comparação a espaços de menor dimensão, desde que o espaço não esteja excessivamente povoado.

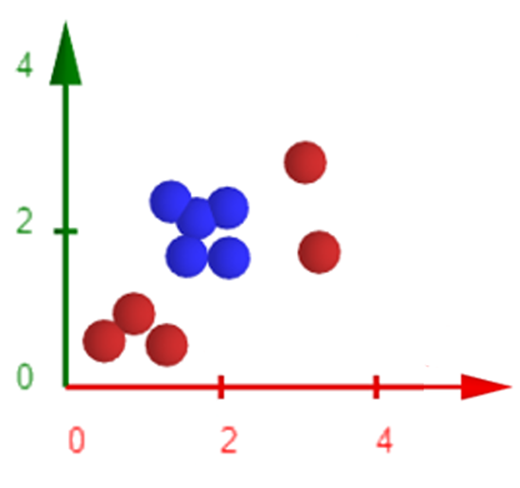
Com base nisso, podemos aplicar uma transformação nos dados, como a função , para mapeá-los em um espaço de características de maior dimensão. Assim, torna-se viável aplicar o SVM linear nesse novo espaço de características.

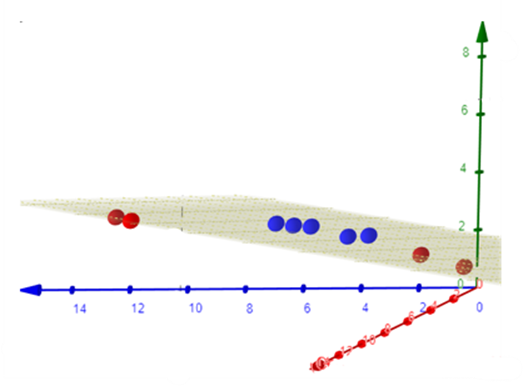
No entanto, é importante observar que o cálculo da função de mapeamento para o espaço de características pode ser computacionalmente custoso devido à alta dimensionalidade.

Truque do Kernel:

O truque do Kernel é uma técnica que nos permite evitar o mapeamento explícito dos dados para o espaço de características de alta dimensão.

Pelo Teorema de Mercer, a função Kernel recebe os pontos do espaço de entrada e calcula o produto escalar entre eles no espaço característica, desde que defina Kernel como matriz positivamente definida e que tenha autovalores maior do que zero.

Exemplificando, temos o kernel que define o mapeamento ϕ para uma dimensão de espaço mais alta. Considere o seguinte:

O mapeamento dos pontos para uma dimensão de espaço mais alta, é dada pela função:

Existem vários tipos de funções Kernel, como o polinomial, o radial e o de tangente hiperbólica. Essas funções definem o mapeamento para uma dimensão de espaço mais alta.

Polinomial

Radial

Tangente hiperbólica

Mas se tivéssemos mais de 2 classes para classificar?

Classificação SVM Multiclasse:

O SVM é originalmente projetado para classificação binária. No entanto, existem métodos que permitem a classificação de mais de duas classes.

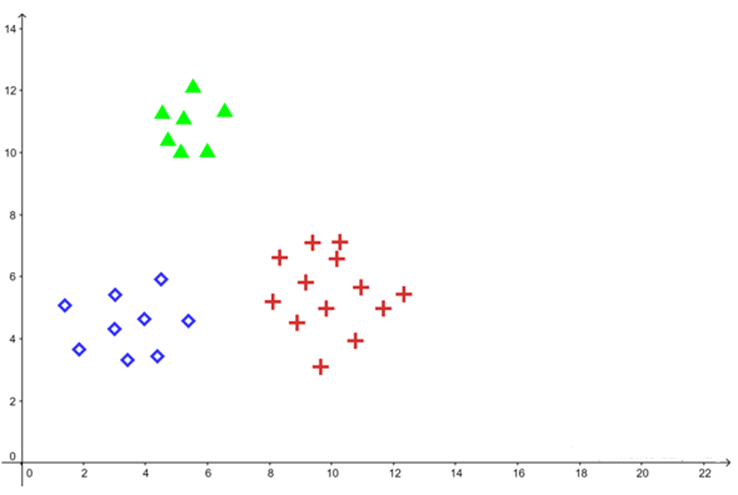
Alguns dos principais métodos são:

Um-contra-todos:

Divide os dados em dois grupos, onde um grupo é formado por uma classe específica e o outro grupo contém todas as outras classes. Isso é repetido para cada classe.

Um-contra-um:

Calcula a classificação entre uma classe e outra classe. Isso é repetido para todos os pares possíveis de classes.

DAG-SVM:

É uma generalização da árvore de decisão, onde a árvore cresce por exclusão de classes, utilizando classificação binária.

Neste post, exploramos de forma acessível e descomplicada o funcionamento do algoritmo de Máquina de Vetores de Suporte (SVM) para problemas de classificação. Espero que você tenha compreendido a lógica por trás desse poderoso algoritmo e esteja pronto para aprofundar seu conhecimento ou até mesmo aplicá-lo em suas próprias tarefas.

Gostaria de ouvir você! Deixe seus comentários abaixo e compartilhe suas dúvidas, experiências ou qualquer insight adicional relacionado ao tema do post. Estou aqui para ajudar e adoraria iniciar uma conversa significativa com nossos leitores. Sua participação é valiosa e contribui para o enriquecimento da comunidade.

Referências:

• Shalev-Shwartz, Shai, and Shai Ben-David. Understanding Machine Learning: From Theory to Algorithms. Cambridge University Press, 2014. [link]

• Faceli, Katti. Inteligência artificial: uma abordagem de aprendizado de máquina. Grupo Gen - LTC, 2011.

• Cover, Thomas M. “Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition.” IEEE Transactions on Electronic Computers, vol. EC-14, no. 3, June 1965, pp. 326–34. DOI.org (Crossref), https://doi.org/10.1109/PGEC.1965.264137. [link]

• Chih-Wei Hsu and Chih-Jen Lin. “A Comparison of Methods for Multiclass Support Vector Machines.” IEEE Transactions on Neural Networks, vol. 13, no. 2, Mar. 2002, pp. 415–25. DOI.org (Crossref), https://doi.org/10.1109/72.991427.

• Platt, John and Cristianini, Nello and Shawe-Taylor, John. “Large Margin DAGs for Multiclass Classification”. Advances in Neural Information Processing Systems, MIT Press, vol.12, 1999. [link]

• V.N. Vapnik and A.Ya. Chervonenkis. Theory of Pattern Recognition. Nauka, Moscow, 1974. (in Russian); German translation: Theorie der Zeichenerkennung, Akademie Verlag, Berlin, 1979.